Česká a slovenská psychiatrie

Časopis
Psychiatrické společnosti ČLS JEP
a Psychiatrickej spoločnosti SLS
souborný článek / review article
URČENÍ ROZSAHU SOUBORU A POWER ANALÝZA V PSYCHIATRICKÉM VÝZKUMU
SAMPLE SIZE DETERMINATION AND POWER ANALYSIS IN PSYCHIATRIC AND PSYCHOLOGICAL RESEARCH
Radek Ptáček, Jiří Raboch
Psychiatrická klinika 1. LF UK a VFN, Praha
SOUHRN
Ptáček R, Raboch J. Určení rozsahu souboru a power analýza v psychiatrickém výzkumu
Určení správné velikosti souboru je základní otázkou jakéhokoliv výzkumu. Nevhodně, nedostatečně nebo naopak nadbytečně stanovený vzorek může zásadním způsobem ovlivnit kvalitu a správnost výsledků, ale i jeho nákladnost a využitelnost obecně. Článek předkládá základní souhrn problematiky power analýzy a určování velikosti souboru s ohledem na specifika psychiatrického a psychologického výzkumu.
Klíčová slova: power analýza, určení rozsahu souboru, psychiatrický výzkum.
SUMMARY
Ptáček R, Raboch J. Sample Size Determination and Power Analysis in Psychiatric and Psychological Research
Proper sample size determination is the basic question of any research. Improperly or insufficiently determined sample may substantially influence quality and correctness of the results, its use in general and its expensiveness too. The article gives basic review of power analysis and sample size determination in psychiatric and psychological research.
Key words: power analysis, sample size determination, psychiatric research.
ÚVOD
Jedním z prvních kroků v jakémkoliv výzkumu je sběr dat u reprezentativního vzorku určité populace. Dalším krokem je pak zjistit, jak se například jistý znak vyskytuje ve sledované skupině, jaký má určitá intervence efekt nebo jaký je vztah mezi sledovanými veličinami, a to s přijatelnou pravděpodobností statistické chyby.14,15,23 Každý výzkum je pokusem o zjištění pravého stavu věcí (například zda je léčba A lepší než léčba B, zda existuje genetická komponenta určitého onemocnění apod.). Vzhledem k tomu, že je obvykle nemožné nebo neproveditelné otestovat každou osobu ve sledované populaci, výzkum obvykle zahrne pouze určitou skupinu probandů, která je vůči základní populaci ve větší či menší míře ideální. Nicméně bez ohledu na charakter a cíle výzkumu, naprosto zásadním kritériem, které následně určí i využitelnost získaných dat, je stanovení dostatečného rozsahu souboru, síly testu (power) a hladiny statistické významnosti.2,3,4,6,19 Při nedostatečně stanovených vstupních parametrech výzkumu mohou být výsledky vyhodnoceny jako statisticky významné, zatímco daná významnost je způsobena pouze náhodou, chybou vyplývající ze způsobu výběru vzorku nebo jinými vlivy. Za tímto účelem je nezbytně nutné stanovit velikost vzorku, který umožní studovanou skutečnost ověřit s přijatelnou statistickou významností a dostatečnou "power".3,4 K tomu slouží celá řada statistických metod, které i přes řadu odlišností vycházejí ze stejných principů statistického uvažování. V předkládaném článku podáváme základní přehled uvedené problematiky s ilustrací na nejběžnějším typu výzkumného projektu v psychiatrii, a to porovnání dvou skupin.19 Článek primárně směřuje k popsání základních principů a souvislostí power analýzy a stanovení velikosti souboru v psychiatrickém a psychologickém výzkumu, jejichž pochopení umožní nejen realizaci těchto metod, ale také kritičtější pohled na výsledky kvantitativních výzkumných studií. Článek podává nejprve přehled základních statisticko-metodologických souvislostí power analýzy a následně pak rozebírá druhy, mechanismy a způsoby jejího výpočtu.
V článku jsou jako příklady uvedené některé výzkumné studie publikované v domácích nebo zahraničních časopisech. Tyto práce autoři záměrně necitují, protože by vzhledem k řadě dalších studií s chybnou statistikou byly znevýhodněny. Tyto studie jsou uvedeny pouze jako příklady a v textu jsou odlišeny kurzivou. Některá uváděná statistická terminologie často prozatím nemá český konsensuální překlad, a proto je uváděna její anglická forma. Použité překlady jsou uvedeny především pro účely lepšího pochopení.
Kvantitativní výzkum, jeho předpoklady a souvislosti
Jedním ze základních prvků kvantitativního výzkumu je stanovení hypotézy a její následné statistické testování.14 Jde tedy o vytvoření předpokladu určitého stavu věcí a jeho následné matematické ověření, s jakou mírou pravděpodobnosti se daný model blíží předpokládané skutečnosti. Tento proces je samozřejmě ovlivněn velkou řadou více či méně podstatných faktorů. V procesu samotného statistického ověřování platnosti hypotézy je zcela fundamentální otázkou, do jaké míry může daná analýza přinést výsledek, který je v rozporu s realitou, a je tedy mylný. V tomto smyslu je několik parametrů, které hrají zcela zásadní roli v pravděpodobnosti, že závěr realizovaného výzkumu se bude blížit k realitě s alespoň přijatelnou a známou možností chyby. Na samém počátku hraje roli stanovení hypotézy samotné. Hypotéza musí vždy vycházet z dobré aktuální znalosti dané problematiky, aby bylo možné odhadnout, jaký předpoklad z kvantitativního hlediska budeme ověřovat.14,15,23 Musíme tedy alespoň odhadnout, např. jakou úroveň sledované proměnné, její změnu nebo vztah ve zkoumaném souboru očekáváme a jakou budeme hodnotit jako klinicky významnou. Stanovujeme tedy minimální klinicky přijatelnou velikost účinku, anglicky "effect size". Dále musíme stanovit přijatelnou hladinu statistické významnosti, a to vzhledem ke dvěma základním typům statistických chyb (I. a II. druhu), a samozřejmě také musíme vědět, jak velký výzkumný vzorek potřebujeme, abychom daný předpoklad prokázali.18,19
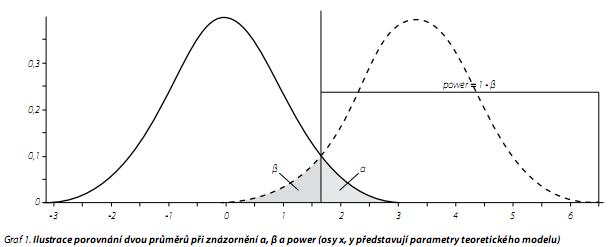
Effect size (velikost účinku)
Effect size (dále jen "ES"), jak jsme již uvedli, je minimální rozdíl mezi sledovanými hodnotami. Například ve sledovaných skupinách, mezi sledovanými časovými úseky apod. Dále například v průměrném skóre dotazníku ve skupině s medikací a bez medikace. Tento rozdíl samozřejmě může nabývat celou řadu hodnot, ale v případě vědecké studie je zapotřebí stanovit minimální rozdíl, který lze považovat za klinicky významný. ES je totiž základním vstupním parametrem pro výpočet tzv. power (síly testu). Obecně platí, že čím větší je ES (tedy rozdíl ve sledované proměnné mezi studovanými skupinami), tím menší vzorek budeme potřebovat. Z grafu 1, který daný vztah ilustruje, je zřejmé, že i malá změna v ES může mít vliv na velikost potřebného vzorku. ES je standardizovaným parametrem, který dílčím způsobem kompenzuje použití různých nástrojů v různých výzkumech. Například umožňuje porovnat dosažené změny v léčbě deprese ve dvou studiích, kdy jedna používá Hamilton Anxiety Scale (HAS) a druhá Montgomery-Asberg Depression Rating Scale (MADRS). Skóre HAS může nabývat hodnot od 0 do 52 a je založené na 13 položkách, zatímco MADRS nabývá hodnot od 0 do 6, při 2bodovém kroku, a vychází z 10 položek. Při srovnání je nepravděpodobné, že by stejné absolutní bodové hodnoty měly stejnou vypovídající schopnost. ES tuto obtíž částečně kompenzuje tím, že transformuje dané výsledky do hodnoty vyjádřené v jednotkách standardní odchylky. ES se obecně vypočítává (vzorec 1):
kde XT je průměr základní skupiny (skupiny, ve které se očekává změna), XC je průměr kontrolní skupiny, SDC je standardní odchylka kontrolní skupiny. V případě, že je power analýza prováděna retrospektivně (viz dále), hodnoty výše uvedených parametrů by měly být uvedeny v závěrečné zprávě nebo vědecké publikaci. Jestliže je však prováděna a priori, popřípadě post hoc, je nutné teoreticky určit minimální rozdíl mezi skupinami, který lze považovat za klinicky významný. Při dostatečném rozsahu vzorku může být jakýkoliv rozdíl statisticky významný, ačkoliv velikost této významné změny může být natolik malá, že již bude i mimo jakoukoliv klinickou významnost.19
Příklad 1: Jistá multicentrická studie prokázala na vzorku 400 osob, že 5 psychoterapeutických sezení vedlo ke snížení skóre v dotazníku HAS o 0,2 standardní odchylky v porovnání se standardní farmakologickou léčbou. Tato změna vyšla na vysoké hladině statistické významnosti a autoři studii uzavřeli konstatováním, že 5 psychoterapeutických sezení je účinnějších v léčbě deprese než antidepresiva, a to i přes fakt, že zjištěná změna, byť statisticky významná, je z klinického hlediska zcela zanedbatelná.
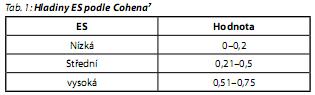
Proto je zde důležité zdůraznit, že rozhodnutí o velikosti minimální hodnoty ES je primárně klinické, nikoliv statistické. Není proto možné jednoznačně určit, co je dostatečná ES a co již nikoliv. Příslušná velikost změny musí být posouzena vzhledem k nástroji, prostřednictvím kterého ji posuzujeme, jevu, který posuzujeme, ale například i vzhledem k nákladnosti léčby. Toto rozhodnutí je tedy zvláště v psychiatrii především otázkou klinického úsudku. Cohen, který problematiku power analýzy uvedl do odborné literatury, stanovil tři základní hladiny ES, které jsou uvedeny v tab. 1 a které je možné v tomto kontextu brát jako orientační.12,16,19
Nulová hypotéza
Hypotéza je predikce vztahu mezi dvěma nebo více proměnnými a je zcela nezbytným východiskem jakéhokoliv kvantitativně založeného výzkumu.12,17 Logika statistické interference požaduje, aby základní hypotéza vycházela z předpokladu, že mezi sledovanými proměnnými není žádný vztah nebo není rozdíl. Takovéto vymezení se označuje jako "nulová hypotéza" (H0). Veškeré další statistické uvažování, plánování, ale i interpretace statistických výsledků vychází z tzv. logiky nulové hypotézy. Špatně formulovaná nulová hypotéza nebo mylná interpretace "statistické významnosti" může zcela obrátit výsledky výzkumu.23
Příklad 2: Výzkum publikovaný v psychiatrickém recenzovaném časopise o vlivu určitého antipsychotika na IQ. Autoři v této studii správně stanovili nulovou hypotézu - "léčba farmakem XY nemá vliv na IQ". Pro zjištění rozdílu použili správný statistický test, nicméně jeho závěry z důvodu nepochopení "testování" nulové hypotézy interpretovali zcela mylně: "Výzkum statisticky významně potvrdil, že léčba preparátem XY nemá na výkon v IQ testu vliv (t = 2,256, p < 0,0001)".
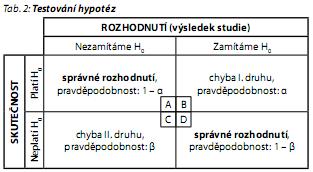
Uvedený výsledek je sice statisticky významný, ale ve smyslu zamítnutí nulové hypotézy. Ve vztahu k danému výzkumu nás informuje, že IQ před a po léčbě se statisticky významně liší. Tedy, že sledovaná léčba má významný vliv na výkon v IQ testu. Podobné výsledky následně mohou vést k mylným rozhodnutím ovlivňujícím léčbu, ale i další výzkum, a ilustrují proto nutnost chápání základních statistických předpokladů a principů v jakémkoliv výzkumu, bez ohledu na obor. Jakýkoliv statistický test tedy představuje metodu ověření nulové hypotézy. Při tomto procesu může dojít k několika skutečnostem, které ilustruje tab. 2. Může nastat případ, kdy naše rozhodnutí je v souladu s realitou. To je samozřejmě jediný žádoucí stav. Dále ovšem může nastat stav, kdy H0 ve skutečnosti platí, ale my jsme ji na základě statistického testu a jeho nastavení zamítli, nebo naopak H0 ve skutečnosti neplatí, ale my jsme ji přesto přijali. Tyto stavy se klasifikují jako statistická chyba I. a II. druhu.
Chyba I. druhu
Nastane-li případ, že testovaná hypotéza je sice pravdivá, ale na základě testové statistiky je zamítnuta (testové kritérium padne do kritického oboru), jde o neoprávněné/ chybné zamítnutí testované hypotézy. Tento případ, v tab. 2 v kvadrantu B, je charakterizovaný jako chyba prvního druhu. Pravděpodobnost této situace, označovaná symbolem "?", je předem vždy známá, a dokonce volitelná - jde o pravděpodobnost odpovídající zvolené hladině významnosti. Nejobvyklejší hladinou významnosti používanou v psychiatrii je 5 % (p = 0,05), což odpovídá pětiprocentní pravděpodobnosti této chyby falešné pozitivity. Použití přísnější hladiny hodnoty "p" na úrovni 1 % (p = 0,01) zvýší velikost požadovaného souboru, ale zároveň významně sníží pravděpodobnost určení nepravdivého výsledku ve smyslu chyby I. druhu.17,19
Chyba II. druhu a power
Nastane-li opačný případ, kdy ve skutečnosti testovaná hypotéza není pravdivá, ale na základě statistického výpočtu dojde k neoprávněnému nezamítnutí nepravdivé testované hypotézy (testové kritérium nepadne do kritického oboru), jedná se o chybu druhého druhu19,23 (v tab. 2 v kvadrantu C). Pravděpodobnost tohoto jevu je označovaná jako "?". Zatímco pravděpodobnost chyby prvního druhu, jak jsme již uvedli, je předem známá a volitelná, chyba druhého druhu je proměnlivá a navíc nepřímo úměrná pravděpodobnosti chyby prvního druhu. V souvislosti s chybou druhého druhu se vyskytuje pojem "power", v české terminologii nejčastěji "síla testu" (pro udržení jednotné terminologie používáme pojem "power"). Power je možné vyjádřit jako 1 - ?, a jde tedy o pravděpodobnost, že test správně identifikuje rozdíl, efekt nebo vztah ve sledovaném vzorku, jestliže existuje (v tab. 2 v kvadrantu D). Jedná se tedy v podstatě pouze o převrácenou logiku chyby druhého druhu. Power, kromě dalších faktorů, závisí na zvolené testové metodě, charakteru rozdělení dat, ale také na skutečných hodnotách parametrů. Proto může být v některých případech obtížné určit chybu druhého druhu na začátku výzkumu. Minimální power v klinických výzkumech se stanovuje na hladině 80 %. To znamená, že jsme ochotni akceptovat 20% pravděpodobnost falešně negativního výsledku. Obvykle se ? stanovuje jako tří- až čtyřnásobek hladiny ?, tedy na úrovni 0,15-0,20, což značí 80-85% power. Cohen7 v tomto kontextu uvádí dvě důležité souvislosti.
1) Zvyšování síly testu (power) vyžaduje poměrně velký nárůst v požadované velikosti vzorku. Například nastavení ? na 0,05 a ? na 0,20 vyžaduje 63 subjektů v každé skupině, aby byla detekována ES s hodnotou 0,50. Při zachování stejné velikosti efektu, ale snížení hladiny ? na 0,10 (tzn. zvýšení power z 80 na 90 %) si toto vynutí zvýšení vzorku o 33% (tzn. na 84 subjektů v jedné skupině).
2) I přesto, že nastavení ? na hladinu 0,80 (80%) se zdá relativně nízké, představuje to oproti běžné praxi, kdy otázka power často není ani zvažována, velice významný pokrok.
Druh statistického testu
Velikost vzorku a následně i power je, kromě výše uvedených parametrů, také ovlivněna typem statistické metody, kterou plánujeme použít. Například parametrické testy (např. t-test) mohou vykazovat lepší schopnost v určování rozdílů v meziskupinových průměrech než neparametrické testy (např. Mannův-Whitneyův U-test), což je také důvod, proč se někdy neparametrická data převádějí do normálního rozložení, a proto budou obecně vyžadovat menší vzorky pro dosažení obdobné významnosti než testy neparametrické.7,19
Velikost vzorku
Velikost vzorku je obvykle uváděna jako N. Čím větším souborem disponujeme, tím menší rozdíly můžeme detekovat. Jinými slovy, čím menší ES očekáváme, tím větší soubor potřebujeme. Určení minimální potřebné velikosti vzorku je základním důvodem a priori realizované "power analýzy". Důvody pro apriorní stanovení minimálního rozsahu vzorku jsou minimálně dva: ekonomický a statistický.4,7,19 Z ekonomického hlediska vyžaduje power analýzu v současné době celá řada poskytovatelů grantové podpory, a to proto, aby bylo jasně stanoveno, kolik probandů je zapotřebí pro prokázání určitého jevu. Stanovení nedostatečného rozsahu vzorku vede ke ztrátě zhodnocení investice vložené do výzkumu, protože výsledky budou v lepším případě neprůkazné, zatímco stanovení přespříliš velkého vzorku vede ke zcela zbytečnému plýtvání finančními prostředky. Statistickým a obecně vědeckým důvodem pro apriorní stanovení minimálního rozsahu zkoumaného souboru je, že malý rozsah vzorku neúměrně zvyšuje riziko chyby II. druhu (ß). Z tohoto důvodu je důkladná power analýza vyžadována i v řadě odborných časopisů.
Power analýza
"Power", jak jsme již uvedli, je pravděpodobnost, že daný statistický test správně identifikuje rozdíl, efekt nebo vztah ve sledovaném vzorku, jestliže existuje (viz např. literaturu4-8,19).
V matematickém vyjádření power = 1 - ?. Grafické znázornění power při testování rozdílu dvou průměrů znázorňuje graf 1. Power je primárně funkcí tří faktorů:
1. Velikosti účinku (ES),
2. hladiny významnosti (?),
3. velikosti vzorku (n).8
Dále také úzce souvisí s typem statistického testu, který bude použit. Power analýzu v tomto smyslu můžeme provést prospektivně (a priori power analýza), což je v moderním výzkumu žádoucí a mnohdy i povinné, a zpětně (retrospektivní a post hoc power analýza), to zvláště v případech, kdy si nejsme jisti skutečnou významností publikovaných výsledků. Realizovat lze i tak zvanou kompromisní power analýzu, kterou lze vypočítat prospektivně i retrospektivně.9-11,24
A priori power analýza7 je postup, kdy velikost vzorku (N) je vypočítána jako funkce požadované úrovně power (1 - ?), předem specifikované hladiny významnosti (?) a velikosti účinku (ES) ve sledované populaci.10,11 A priori power analýza by měla být základním předpokladem jakéhokoliv moderního výzkumu.18
Post hoc power analýza7 je na rozdíl od předchozího případu realizována až po samotném výzkumu. Při post hoc analýze je power vypočítána jako funkce použité hladiny významnosti (?), populační velikosti účinku (ES) a použité velikosti souboru (N). Tato analýza tak umožňuje zhodnotit, zda publikovaný statistický test měl šanci odmítnout nesprávnou H0. Důležité je zdůraznit, že post hoc analýza, obdobně jako a priori analýza, vyžaduje, aby ES vycházel z teoretického odhadu jeho velikosti v základní populaci, nikoliv dosažené ES ve sledovaném souboru. V tomto se post hoc power analýza liší od poměrně diskutované retrospektivní power analýzy, která vychází z předpokladu, že ES ve zkoumaném souboru je identická s ES v základní populaci.26 Tento předpoklad je z klinického i statistického hlediska nejednoznačný a je předmětem kritiky celé řady autorů.13,22 V tomto smyslu je metodologicky a klinicky správným postupem v případě potřeby provést power analýzu zpětně, vyjít z teoreticky odhadované ES s klinickou významností a retrospektivní analýzu pak provádět pouze v případech, kdy je oprávněný předpoklad shody ES dosažené ve výzkumu a ES teoreticky předpokládané, nebo v případech, kdy ES není vzhledem k novosti výzkumu nebo jiným důvodům možné odhadnout.19
Kompromisní power analýza ("compromise power analysis")9,10 je postup, kdy hladina významnosti (?) i power (1 - ?) jsou vypočítány jako funkce ES, velikosti souboru (N) a koeficientu pravděpodobnosti chyby (q = ?/?). Použití a nastavení kompromisní analýzy je možné ilustrovat např. nastavením q = 1, což znamená, že výzkumník preferuje vyrovnané riziko chyby I. a II. druhu (? = ?), zatímco q = 4 znamená, že ? je čtyřikrát menší než alfa (? = 4.).7 Kompromisní power analýza může být použita apriorně i zpětně. Apriorně může být použita například v případě, kdy výzkumník je limitovaný určitou maximální velikostí vzorku, kterou kvůli nákladům nebo jiným důvodům nemůže překročit. Obdobně je tomu, jestliže studie již realizována byla a autor se ptá po reliabilním rozhodovacím kritériu, které zajistí přiměřeně vyrovnané riziko při dané velikosti souboru a ES, kterou stanovil. Je zřejmé, že kompromisní power analýza takto může vyústit v jiné než standardní hladiny významnosti (? = 0,05 a ? = 0,01), nicméně tento fakt je vyrovnaný získanou rovnováhou rizika chyby I. a II. druhu. Power analýzu a stanovení velikosti souboru lze provést v zásadě třemi způsoby:
1) Přímým výpočtem. Tento postup poskytuje největší kontrolu nad celým procesem výpočtu, může být ovšem v některých případech studií, zvláště se složitějším designem, poměrně obtížný.
2) Využití některých ze standardizovaných nomogramů1,16 nebo tabulek navržených pro tyto účely (viz např. graf 1 a tab. 3). Jde o velice rychlou metodu, o které se dále krátce zmíníme, která ovšem vykazuje nejmenší přesnost a je zatížena řadou možných chyb.
3) Prostřednictvím statistických programů. Dnes se jedná o nejčastější cestu power analýzy a stanovení velikosti souboru. V současné době existuje velké množství programů, které tyto úkony nabízejí v uživatelsky velice přívětivé formě. Nicméně i statistické programy vyžadují zadání základních parametrů, kterým je zapotřebí rozumět. Přestože se tímto postupem můžeme rychle dobrat k výsledkům s nejvyšší přesností, zadání vstupních údajů bez hlubšího porozumění principu daných mechanismů může naopak vést k získání mylných údajů. Možnosti výpočetní realizace power analýzy krátce zmiňujeme v závěru článku.
Výpočet velikosti vzorku
Od 70. let 20. století se problematikou stanovení minimální velikosti vzorku zabývalo mnoho autorů, kteří nabídli různé přístupy pro různé typy designů výzkumných studií.20,21,24 I přes řadu zcela nových studií a publikací mezi základní autory v této oblasti patří Cohen.4-8
Vzhledem k tomu, že tato práce nemůže podat přehled všech aktuálních přístupů ke stanovení velikosti souboru u různých designů vědeckých studií a statistických testů, předkládáme ilustraci postupu pro psychiatrii nejčastějšího typu studie. Tím je porovnání průměrů hodnot určité veličiny v jedné nebo ve dvou skupinách (např.: porovnání biochemických výsledků před léčbou a po ní; porovnání výsledků určitého psychologického testu např. u osob s psychotickými projevy a u osob bez nich), nebo se může porovnávat poměr osob ve dvou skupinách (např. poměr osob s vedlejšími účinky u léku A a léku B).20, 23
První případ patří mezi nejčastější typy výzkumných studií nejen v psychiatrii a psychologii, ale v medicíně a společenských vědách obecně. Výstup je zde měřen nejčastěji na různých škálách, prostřednictvím psychologických testů nebo různých biologických parametrů. Výsledkem je obvykle celočíselná hodnota, která vyjadřuje úroveň zkoumaného jevu. Vzorec 1 je nejčastějším a nejjednodušším způsobem stanovení potřebného vzorku v tomto případě.
Vzorec 2 slouží ke stanovení velikosti vzorku při porovnávání průměru dvou skupin. V tomto vzorci je ? rozdíl mezi průměry sledovaných proměnných, ? je standardní odchylka, z?, z? jsou hodnoty z tabulek normálního rozložení s cílem stanovení chyby I. a II. druhu. Hodnoty z?, z? pro nejpoužívanější hodnoty u párového t-testu jsou uvedeny v tab. 3. Kompletní tabulky jsou obvykle uváděny ve statistických učebnicích. Je důležité poznamenat, že pro výpočet velikosti souboru podle výše uvedeného vzorce není nezbytně nutné znát přesnou hodnotu parametrů ? a ?.4-8,14,19 Vzhledem k tomu, že ?/? je pouze inverzí k hodnotě ES (ES= ?/?), mohou být použita jakákoliv dvě čísla, která vyjadřují tento poměr. Pro zjednodušení výpočtu je vhodné například v případě ES 0,5 nastavit parametry: ? = 2 a ? = 1; výpočet podle tohoto vzorce lze tedy použít, jsou-li stanoveny parametry ?, ?, nebo - jak je demonstrováno výše - alespoň ES.
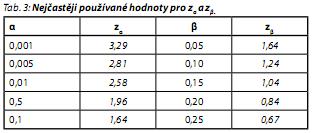
Příklad 3: Pro ilustraci výše uvedeného případu lze použít hypotetický příklad studie porovnávající efektivitu antidepresiv u dvou skupin probandů. Efektivita je měřena dotazníkem, kdy za minimální významný rozdíl jsou považovány 4 body (tzn. ? = 4), kdy standardní odchylka je na základě předchozích zkušeností s dotazníkem předpokládána na úrovni 8 bodů (tzn. ? = 8). Hladina významnosti je nastavena na 5% (tedy ? = 0,05) a power na 20% (tedy ? = 0,20). Z tabulky na základě tohoto údaje doplníme hodnoty z? = 1,96 a z? = 0,84. Celý vzorec bude následně vypadat takto:
Z dosazené rovnice (vzorec 2) je zřejmé, že pro výše uvedený výzkumný projekt budeme potřebovat 63 probandů na jednu skupinu, celkově tedy alespoň 126. Jestliže hodnota N nevyjde jako desetinné číslo, vždy se zaokrouhluje nahoru. Uvedený vzorec názorně ilustruje výše uvedené vztahy parametrů N, ?, ? a v podstatě i ES. V případě, že bychom požadovali vyšší power např. na úrovni 0,05, byla by hodnota z? = 1,64 a minimální požadovaná velikost vzorku by vzrostla na 104 probandů ve skupině (celkové N = 208). Obdobně kdybychom chtěli určit statistickou významnost menšího rozdílu, například dvou bodů, narostl by nám celkový požadovaný rozsah celého souboru na 502 při ? = 0,20, a při ? = 0,05 dokonce na 830.
Dalším případem, který uvedeme, je potřeba porovnání proporcionality subjektů ve dvou skupinách, které vykazují určité změny, jako je například změna po léčbě, rozvoj vedlejších účinků, sebevražedné sklony apod. Pro tyto příklady existuje celá řada výpočetních postupů, které mohou vykazovat poměrně odlišné výsledky. Nejjednodušším a často také nejpoužívanějším postupem je:19
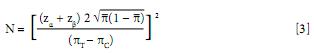
Vzorec 3 slouží ke stanovení velikosti vzorku při porovnávání proporcionality subjektů ve dvou skupinách. V tomto vzorci je ?T poměr subjektů v experimentální skupině (skupina s léčbou, intervencí apod.), u které se očekává určitý výsledek, a ?C je poměr v kontrolní skupině, ? je celkový průměr, tzn.
Parametry z?, z? mají stejný význam jako výše.
Příklad 4: Pro ilustraci daného výpočtu můžeme uvést příklad, kdy u farmaka A je známý výskyt nežádoucích vedlejších účinků přibližně u 20% pacientů. U nového léku B je předpoklad, že tyto vedlejší účinky se budou vyskytovat maximálně u 10 % pacientů. Základní otázkou je tedy, kolik pacientů je zapotřebí, abychom daný předpoklad ověřili na přijatelné hladině významnosti. Do výše uvedeného vztahu dosadíme ?T = 0,20 a ?C = 0,10 (z toho vyplývá, že ? = 0,15). Při dosazení těchto hodnot dostaneme rovnici:
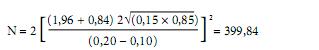
Pro ověření výše uvedeného předpokladu tedy potřebujeme 400 subjektů v každé skupině.
Zpětná power analýza
Post hoc a retrospektivní power analýza může být provedena z mnoha důvodů. Oponent určité studie si chce ověřit, zda byl použit dostatečně velký soubor, jaká je pravděpodobnost chyby II. druhu vzhledem k závěrům (zvláště v případech, kdy závěry neprokázaly rozdíl mezi sledovanými veličinami - např. nebyl prokázán efekt léčby, rozdíl mezi skupinami apod.). Zpětná power analýza může být také provedena pro ověření autorova tvrzení o vyrovnanosti skupiny ve smyslu demografických nebo klinických charakteristik, i když postulovaná "ekvivalence" mezi skupinami je často pouze nedostatečná power, která by umožnila detekovat smysluplné rozdíly. Je důležité také zdůraznit, že power analýzu není nutné provádět v případech, kdy byly prokázány rozdíly nebo vztahy mezi sledovanými veličinami. V tomto případě je jasné, že tu byla dostatečná power, která umožnila demonstrovat efekt. To, zda daná velikost efektu je klinicky významná, představuje jinou otázku, která už je předmětem interpretace.9,10,19
Post hoc, případně retrospektivní power analýzu je možné provést minimálně dvěma postupy. Můžeme vypočítat samotnou power studie nebo určit, jak veliký vzorek by byl zapotřebí, aby se v daném případě prokázal významný výsledek. Za tímto účelem je možné použít výše uvedené vzorce č. 1 a 2. Efektivnější metoda je ovšem přímé vypočítání využití zß prostřednictvím vzorce 4, pro případ porovnávání dvou průměrů. Přičemž rozdíl mezi post hoc a retrospektivní power analýzou je, že při počítání hodnoty post hoc power vycházíme z ES teoreticky předpokládané a při retrospektivní aplikujeme hodnoty dosažené v samotném výzkumu.9,19 O rozdílech jsme pojednali výše.
Vzorec 4 je určen pro výpočet z? při porovnávání dvou průměrů, kde p1 je poměr subjektů v první skupině a p2 v druhé. Parametry ? a ? jsou reálnými hodnotami rozdílu průměrů a standardní odchylky uvedené ve výzkumné studii. Jestliže je počet subjektů ve sledovaných skupinách přibližně stejný, je možné vzorec zjednodušit (vzorec 5):
Z vypočítané hodnoty zß se za pomoci tabulek najde příslušná hodnota ?.
Příklad 5: Jako příklad pro retrospektivní analýzu použijeme příklad studie, která si kladla za cíl prokázat, že není rozdíl mezi chlorpromazinem (CPZ) a placebem v potlačování schizofrenních symptomů. Jako míra hodnocení byla zvolena hodnoticí škála BPRS. Ve studii bylo zařazeno pouze 18 pacientů v placebo skupině a 18 pacientů s CPZ. I přesto výsledky byly negativní, a je zde proto podezření na chybu II. druhu. Z dat uvedených ve studii vyčteme, že hodnota ? = 8,91, ? = 0,05, což podle tabulek znamená z? = 1,96. Proto, aby byla detekována ES alespoň 0,5 v BPRS, by musel být rozdíl alespoň 4,45. Celkový počet subjektů tedy byl 34. Vzhledem k tomu, že skupiny byly téměř rovnocenné, je možné použít vzorec 5. Na základě dosazení uvedených čísel dostaneme:
Výsledek vyhledáme ve statistických tabulkách a zjistíme, že vypočítaná hodnota ? = 0,25. Můžeme tedy uzavřít, že power pro detekci ES 0,5 mezi CPZ a placebem byla menší než 75 %. V souvislosti s touto studií tedy můžeme konstatovat, že je nejen mimo jakoukoliv statistickou, ale i klinickou významnost, ale také, že uvádí poměrně zavádějící a nepodložené závěry.
Jestliže potřebujeme vypočítat power u dvou proporcí, vzorec je:

Příklad 6: V další obdobné studii autoři uzavírají, že mezi skupinami nebyl shledán rozdíl v počtu vedlejších účinků. V této souvislosti můžeme vypočítat power pro snížení vedlejších účinků z 50% (?T = 0,5) v CPZ skupině na 25 % ve skupině s propanolem (?T = 0,25). Vzhledem k neúplným datům v první skupině bylo pouze 11 subjektů a ve druhé 13 (N = 24). Dosazením do rovnice dostaneme:
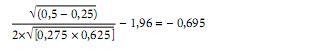
Opět vyhledáme hodnotu ve statistických tabulkách (jestliže je hodnota z ? negativní, vyhledáme její absolutní hodnotu) a zjistíme, že se s obtížemi blíží hodnotě power 20 % (? je v tomto případě 0,75), což je velice neuspokojivý výsledek. Na základě výše uvedených výpočtů zjistíme, že pro prokázání výsledku s alespoň 80% power bychom potřebovali 77 subjektů v každé skupině, tedy celkové potřebné N = 144 vůči aktuálně použitému N = 24. Vzhledem k tomuto výraznému poddimenzování i kriticky nízké power jsou výsledky studie zcela mimo jakoukoliv interpretovatelnost.
Bezvýpočtové stanovení velikosti vzorku
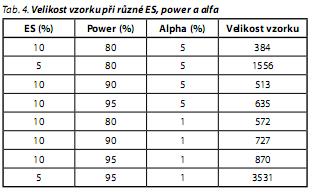
V praxi je možné stanovení velikosti vzorku i bez výpočtu nebo využití výpočetní techniky. Pro tento případ existují tabulky a speciální nomogramy, které lze najít v různých statistických učebnicích nebo publikacích.1,16 Při použití těchto technických pomůcek je nicméně také nutné odhadnout alespoň přibližnou hodnotu ES, stanovit hladinu ? a samozřejmě také power. Na základě této kombinace můžeme v příslušné tabulce nebo v nomogramu vyčíst potřebný vzorek. Tab. 4 takovou možnost ilustruje. V prvních třech sloupcích si nalezneme požadovanou kombinaci parametrů a ve čtvrtém najdeme příslušnou hodnotu pro rozsah souboru.
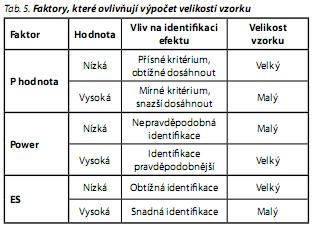
Graf 2 ilustruje o něco pružnější možnost stanovení velikosti vzorku na základě pro tyto účely vytvořeného nomogramu. Nomogram dle Altmana a Gora1 je právě v oblasti psychiatrického a psychologického výzkumu uváděn nejčastěji. Na levé ose nomogramu se najde příslušná hladina ES, na pravé pak power. Na spojnici těchto hodnot poté nalezneme hodnotu pro potřebnou velikost vzorku na hladině významnosti 0,01 a 0,05. Základním limitem těchto metod ovšem je, že pracují pouze s předem stanovenými hodnotami, a nelze z nich proto určit potřebnou hodnotu pro konkrétní případ. Jsou tedy zatíženy určitou nepřesností, která se pak pochopitelně může odrazit i ve výsledcích realizované studie (tab. 5). Tyto postupy tedy doporučujeme pouze jako krajní případ nebo rychlý způsob orientace při rámcovém plánování budoucího výzkumu, kdy při rozhodnutí o realizaci bude velikost vzorku vypočítána přesně.23
Příklad 7: Graf 3 je ilustrací, jak stanovit velikost vzorku při požadovaných parametrech, ES = 0,78 a power = 80 %. Pro mírnější úroveň statistické významnosti ? = 0,05 bude dostatečný vzorek přibližně N = 52, při významnosti ? = 0,01 bude zapotřebí pro prokázání stejného efektu vzorek již N = 74.
Metody počítačové analýzy
V současné době je pro účely power analýzy a stanovení velikosti vzorku celá řada počítačových programů. V podstatě všechny běžně dostupné komerční programy umožňují rozsáhlé a podrobné analýzy. Nicméně i mezi volně dostupnými nástroji lze najít celou řadu kvalitních programů, které umožňují dané analýzy s reliabilními výsledky. Mezi nejčastěji používané patří například G*Power, vyvinutý a průběžně aktualizovaný Institutem experimentální psychologie Univerzity Heinricha Heineho v Düsseldorfu, který je volně dostupný na internetu.27 Program umožňuje detailní power analýzu pro nejčastěji používané statistické testy (t-test, f-test, korelace, ANOVA, mnohočetné korelace a regrese, chí?-test, kontingenční tabulky), a to pro případy post hoc i a priori power analýzy, ale i pro případ power analýzy kompromisní. Analýza, podrobný popis a možnosti použití tohoto programu byly opakovaně publikovány v odborné literatuře.9-11 Mezi dalšími možnostmi lze zmínit statistické on-line nástroje různých světových univerzit, které jsou pro vědecké účely volně dostupné. Např. University of California, Los Angeles,28 University of Iowa29 a podobně.
DISKUSE
Parametrické a transparentní plánování vědeckého výzkumu je v současné odborné literatuře zcela jednoznačným trendem.1,4-7,19,22,28 Power analýza a stanovení rozsahu vzorku je implicitním předpokladem pro podporu ze strany řady grantových institucí nebo publikaci v odborných časopisech.7,19 Základní znalost principů kvantitativního výzkumu a testování hypotéz by měla být dnes zcela samozřejmou pro všechny vědecké pracovníky. Přesto je možné setkat se se studiemi, které redukují statistickou významnost pouze na hodnotu "p", která v některých případech není uvedena ani formálně správně.12,14,19 Tato praxe vede nejen k publikaci nerelevantních poznatků, které se pak mohou stát nesprávnými východisky jiných výzkumů, případně klinických rozhodnutí, ale zároveň budují v odborné lékařské veřejnosti mylné přesvědčení o jednorozměrnosti a jednoduchosti pojmu "statistická významnost", která je tak spojována pouze s chybou I. druhu, v odborné literatuře uváděné jako výše uvedené "p".12,19 Uzavírat výsledky jako významné pouze proto, že statistický program na základě výpočtů určí hladinu "p" na velice nízké úrovni (často se setkáme i se zcela nesmyslnými hodnotami jako p < 0,00000000), je stejné, jako kdyby psychiatr diagnózu schizofrenie uzavíral na základě toho, že pacient v prázdné čekárně s někým mluví (aniž by si zjistil, zda nehovoří s někým například mobilním telefonem). Bohužel s tímto přístupem je možné se i dnes setkat v podstatě ve všech vědních oborech, tedy nejen v psychiatrii a psychologii, a to v recenzovaných domácích, ale i zahraničních časopisech. Někdy tak najdeme závěry typu: "Rozdíly před léčbou a po léčbě byly shledány jako statisticky velice významné (p < 0,0000000)". A dále na základě tohoto konstatování autoři dané studie vyvozují poměrně závažné závěry. Ve své podstatě samozřejmě nelze vyloučit, že daný rozdíl je skutečně statisticky významný a zkoumané realitě se přibližuje, nicméně způsob uvedení statistické významnosti nejen informuje o tom, že autoři o pojmu statistická významnost nemají konceptuální představu, ale především takovéto výsledky znemožňují další využití této práce pro jiné autory (např. pro replikace daného výzkumu, pro použití dat v metaanalýze), což daný vědecký výstup znehodnocuje úplně stejně. V této souvislosti je tedy nutné zdůraznit a uzavřít, že důkladné statistické a metodologické ukotvení jakéhokoliv výzkumu je vůbec základním předpokladem vědecké práce, která následně umožní i jeho klinickou interpretaci a využití.7,12-16,19,28
ZÁVĚR
Na počátku jakéhokoliv výzkumu je nutné vypočítat potřebnou velikost souboru pro ověření plánované hypotézy. Příliš malý vzorek vede ke zvýšenému riziku chyby II. druhu, zatímco příliš velký soubor představuje zbytečně vynaložené časové i finanční náklady. Vzhledem k tomu, že negativní výsledky určité studie mohou být pouze chybou II. druhu, i běžný čtenář by měl být schopen odhadnout, zda to, co se jeví klinicky významné, ale statisticky nevýznamné, je pravda nebo ne. Základní výpočet velikosti souboru a power analýza představuje, zvláště s využitím moderních výpočetních programů, poměrně snadné postupy, který by si měl každý výzkumný pracovník osvojit. Zároveň znalost těchto postupů by měla vést i k uvádění potřebných statistických údajů ve výzkumných studiích proto, aby mohly být dále kriticky hodnoceny a využívány v oblasti výzkumné praxe, např. v souvislosti s tolik potřebnými metaanalýzami nebo přímo v klinické praxi.
LITERATURA
- 1. Altman DG, Gore SM. Statistics in practice. Harrow, Middlesex: BMJ; 1982.
- 2. Arkin CF, Wachtel MS. How many patients are necessary to assess test performance? JAMA 1990; 263: 275-278.
- 3. Bach LA, Sharpe K. Sample size for clinical and biological research. Aust N Z J Med 1989; 19: 64-68.
- 4. Cohen J. The statistical power of abnormal-social psychological research: A review. J Abnorm Psychol 1962; 65: 145-153.
- 5. Cohen J. Some statistical issues in psychological research. In Wolman, BB, ed. Handbook of clinical psychology. New York: McGraw-Hill; 1965: 95-121.
- 6. Cohen J. Statistical power analysis for the behavioral sciences. San Diego, CA: Academic Press; 1969.
- 7. Cohen J. Statistical power analysis for the behavioral science. 2nd ed. Hillsdale, NJ: Erlbaum; 1988.
- 8. Cohen J. Things I have learned (so far). Am Psychol 1990; 45: 1304-1312.
- 9. Erdfelder E, Faul F, Buchner A. GPOWER: A general power analysis program. Behav Res Meth Instr Comput 1996; 28: 1-11.
- 10. Erdfelder E, Faul F, Buchner A. Power analysis for categorical methods. In: Everitt, BS, Howell, DC, eds. Encyclopedia of statistics in behavioral science. Chichester, UK: Wiley; 2005: 1565-1570.
- 11. Faul F, Erdfelder E, Lang AG, Buchner A. GPOWER: A general power analysis program. Behav Res Meth Instr Comput 2007; 39 (2): 175-191.
- 12. Gigerenzer G, Krauss S, Vitouch O. The null ritual: What you always wanted to know about significance testing but were afraid to ask. In: Kaplan D, ed. The SAGE handbook of quantitative methodology for the social sciences. Thousand Oaks, CA: Sage; 2004: 391-408.
- 13. Gerard PD, Smith DR, Weerakkody G. Limits of retrospective power analysis. Journal of Wildlife Management 1998; 62: 801-807.
- 14. Howitt D, Cramer D. Introduction to statistics in psychology. Sydney: Pearson Education; 2007.
- 15. Howell DC. Fundamental statistics for the behavioral sciences. 6th ed. Belmont, CA: Cengage Learning; 2007.
- 16. Lwanga SK, Lemeshow S. Sample size determination in health studies: A practical manual. 1st ed. Geneva: World Health Organization; 1991.
- 17. O?Hara J. How I do it: sample size calculations. Clin Otolaryngol 2008; 33 (2): 145-149.
- 18. Keppel G, Wickens TD. Design and analysis. A researcher?s handbook. 4th ed. Upper Saddle River, NJ: Pearson Education International; 2004.
- 19. Streiner DL. Sample size and power in psychiatric research. Can J Psychiatry 1990; 35 (7): 616-620.
- 20. Schlesselman JJ. Case-control studies: Design, conduct and analysis. 1st ed. New York: Oxford University Press; 1982.
- 21. Shieh G. A comparative study of power and sample size calculations for multivariate general linear models. Multivariate Behavioral Research 2003; 38: 285-307.
- 22. Steidl RJ, Hayes JP, Schauber E. Statistical power analysis in wildlife research. Journal of Wildlife Management 1997; 61: 270-279.
- 23. Young MJ, Bresnitz EA, Strom BL. Sample size nomograms for interpreting negative clinical studies. Ann Int Med 1983; 99: 248-251.
- 24. Weiss NA, Weiss CA. Elementary statistics. 7th ed. Upper Saddle River, NJ: Addison-Wesley; 2007.
- 25. Whitley E, Ball J. Statistics review 4: Sample size calculations. Crit Care 2002; 6 (4): 335-341.
- 26. Zumbo BD, Hubley AM. A note on misconceptions concerning prospective and retrospective power. The Statistician 1998; 47: 385-388.
- 27. http://www.psycho.uni-duesseldorf.de/aap/projects/gpower/
- 28. http://socr.ucla.edu/SOCR.html
- 29. http://www.cs.uiowa.edu/~rlenth/Power/





